Ваша мать дает вам 100 долларов наличными на подарок на день рождения и говорит: “Тратьте их с умом”. Вы хотите приобрести новейший сотовый телефон на рынке. Но задаетесь вопросом. Действительно ли это лучшее использование ваших денег. У вас есть выбор: вы можете потратить деньги сейчас или потратить их в будущем. Что вам следует делать? Есть ли польза в том. Чтобы потратить их сейчас. А не откладывать на будущее? Влияет ли время на стоимость ваших денег в будущем? Предприятия сталкиваются с этими и другими вопросами при принятии решения о том. Как распределять инвестиционные деньги. Основным фактором. Влияющим на их инвестиционные решения. Является концепция временной стоимости денег.
Концепция временной ценности денег утверждает. Что стоимость доллара сегодня стоит больше. Чем стоимость доллара в будущем. Обычно это происходит потому. Что доллар сегодня можно использовать сейчас. Чтобы заработать больше денег в будущем. Также, как правило. Существует вероятность будущей инфляции. Которая со временем снижает стоимость доллара и может привести к снижению покупательной способности экономики.
На данном этапе потенциальные последствия инфляции, вероятно. Лучше всего можно продемонстрировать на нескольких примерах.
Первый пример-Ford Mustang. Первый Ford Mustang был продан в 1964 году за 2368 долларов. Самый дешевый Мустанг на сегодняшний день начинается с прейскурантной цены в 25 680 долларов. В то время как значительная часть этого увеличения обусловлена дополнительными функциями на более новых моделях. Большая часть увеличения обусловлена инфляцией. Которая произошла в период с 1964 по 2019 год.
Аналогичные характеристики инфляции можно продемонстрировать и в отношении цен на жилье. После Второй мировой войны типичный небольшой дом часто продавался по цене от 16 000 до 30 000 долларов.
Многие из этих же домов сегодня продаются за сотни тысяч долларов. Большая часть увеличения обусловлена местоположением объекта недвижимости. Но значительная часть также связана с инфляцией. Годовой уровень инфляции для Mustang в период с 1964 по 2019 год составлял примерно 4,5%. Если мы предположим. Что дом был продан за 16 500 долларов в 1948 году. А цена дома в 2019 году составляла около 500 000 долларов. То это ежегодный прирост стоимости почти на 5%.
Сегодняшний доллар также более ценен, потому что существует меньший риск. Чем если бы доллар был вложен в долгосрочные инвестиции. Которые могут принести или не принести ожидаемых результатов.

С другой стороны, отсрочка платежа по инвестициям может быть выгодна, если есть возможность заработать проценты. Чем дольше задерживается платеж. Тем больше возможностей для заработка. Это может быть заманчиво для бизнеса и может убедить его пойти на риск отсрочки.
Компании учитывают временную ценность денег. Прежде чем принимать инвестиционное решение. Они должны знать. Какова будущая стоимость их инвестиций по сравнению с сегодняшней текущей стоимостью и какую потенциальную прибыль они могли бы получить из-за задержки платежа.
Эти соображения включают в себя нынешние и будущие ценности.
Прежде чем вы узнаете о текущих и будущих значениях, важно изучить два типа денежных потоков: единовременные выплаты и аннуитеты.
Единовременная выплата-это единовременная выплата или возврат средств в определенный момент времени. Единовременная сумма может быть как текущей. Так и будущей стоимостью. Для единовременной выплаты приведенная стоимость-это стоимость данной суммы на сегодняшний день. Например, если бы вы сегодня внесли 5000 долларов на сберегательный счет по заданной процентной ставке, скажем. 6%лью вывести их ровно через три года. Сегодняшние 5000 долларов были бы единовременной суммой по текущей стоимости.
Предположим для простоты, что счет выплачивает 6% в конце каждого года, а также начисляет проценты на проценты. Заработанные в предыдущие годы.
В нашем текущем примере проценты начисляются один раз в год. Однако проценты также могут быть рассчитаны различными способами. Некоторые из наиболее распространенных расчетов процентов производятся ежедневно, ежемесячно, ежеквартально или ежегодно. Одна из концепций. Которую важно понимать при расчете процентов. – это концепция компаундирования.

Компаундирование-это процесс получения процентов по предыдущим полученным процентам. А также процентов. Полученных по первоначальным инвестициям.
Возвращаясь к нашему примеру. Если 5000 долларов будет депонировано на сберегательный счет в течение трех лет с ежегодным начислением 6% годовых. Сумма инвестиций в размере 5000 долларов будет равна $5,955.08 ($5,000 × 1.06 – $5,300 × 1.06 – $5,618 × 1.06 – $5,955.08). 5 955,08 доллара-это будущая стоимость 5000 долларов. Инвестированных в течение трех лет под 6%. Более формально будущая стоимость-это сумма. До которой одна или несколько инвестиций будут расти в течение определенного времени по определенной процентной ставке или ставкам.

Первоначальные инвестиции в размере 5000 долларов США представляют собой приведенную стоимость. Опять же, более формально, приведенная стоимость-это текущая стоимость одной будущей инвестиции или серии инвестиций за определенное время по заданной процентной ставке или ставкам. Другой способ сформулировать это так: 5000 долларов-это текущая стоимость 5 955,08 доллара. Когда первоначальная сумма была инвестирована под 6% в течение трех лет. Проценты. Заработанные за трехлетний период. Составят 955,08 доллара. А оставшиеся 5000 долларов составят первоначальный депозит в размере 5000 долларов.
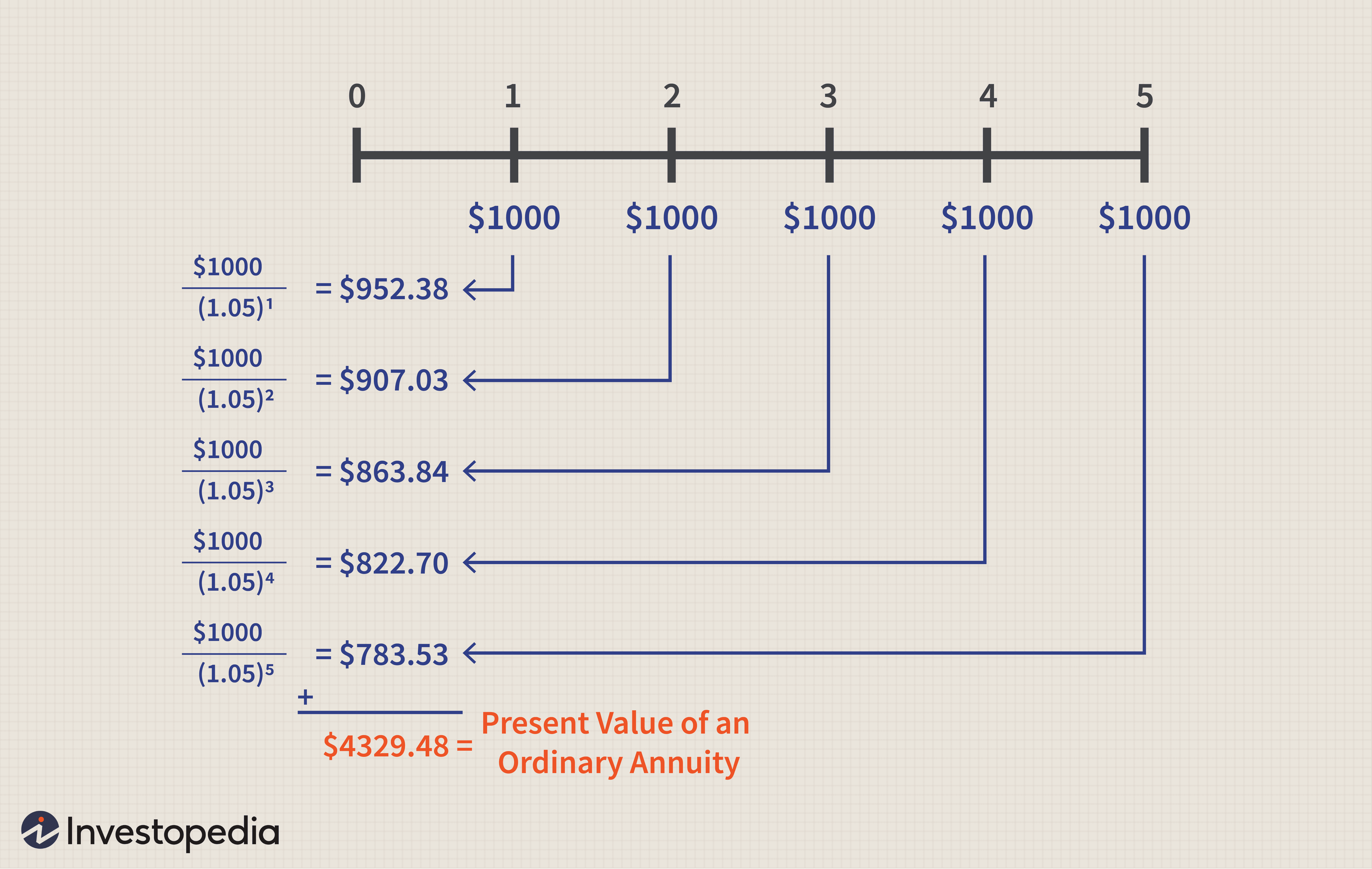
Как показано в примере, будущая стоимость единовременной выплаты-это стоимость данной инвестиции в какой-то момент в будущем. Также возможно проведение серии платежей. Которые представляют собой серию единовременных выплат. Предположим. Что бизнес получает следующие четыре денежных потока. Они представляют собой серию единовременных выплат. Потому что не все они составляют одинаковую сумму.

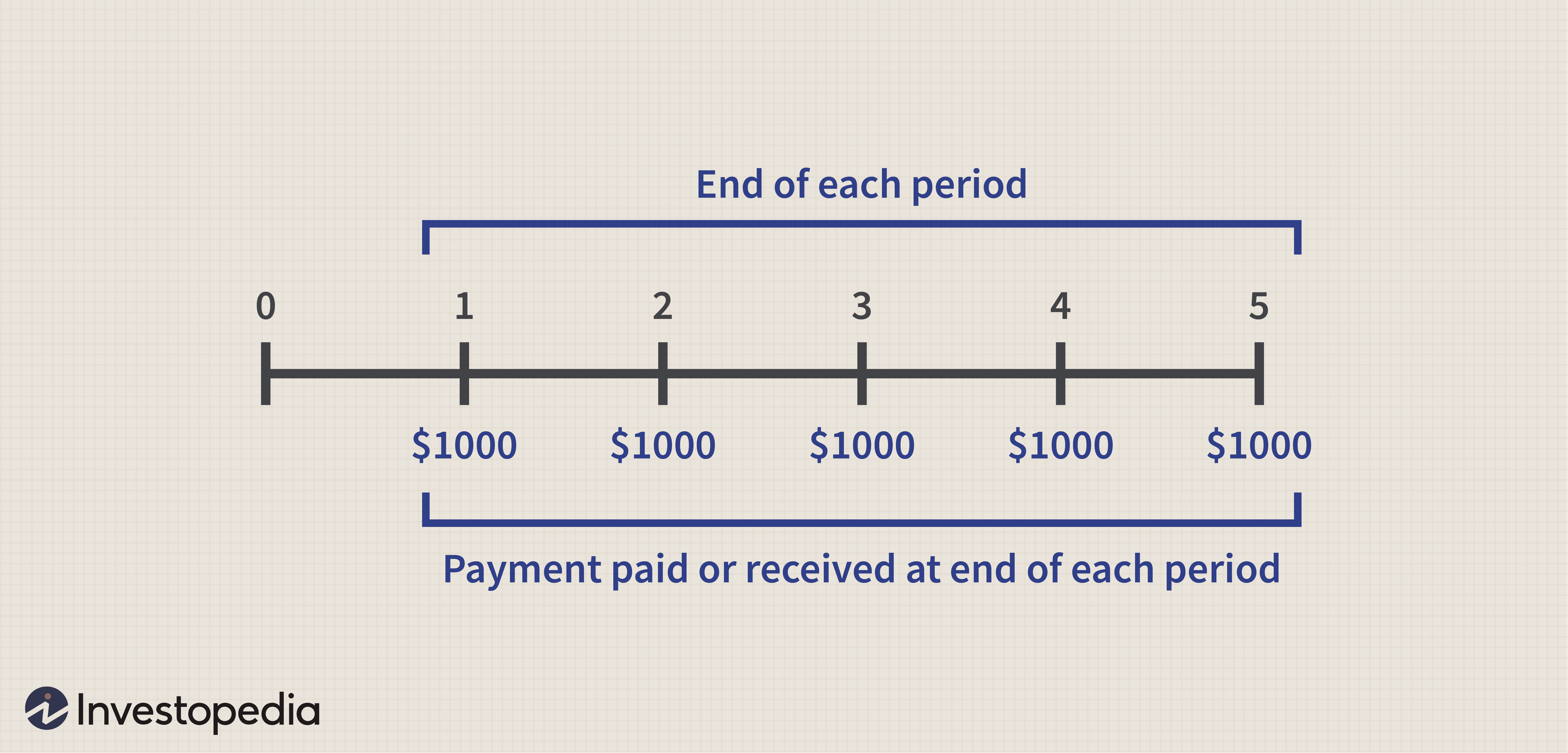
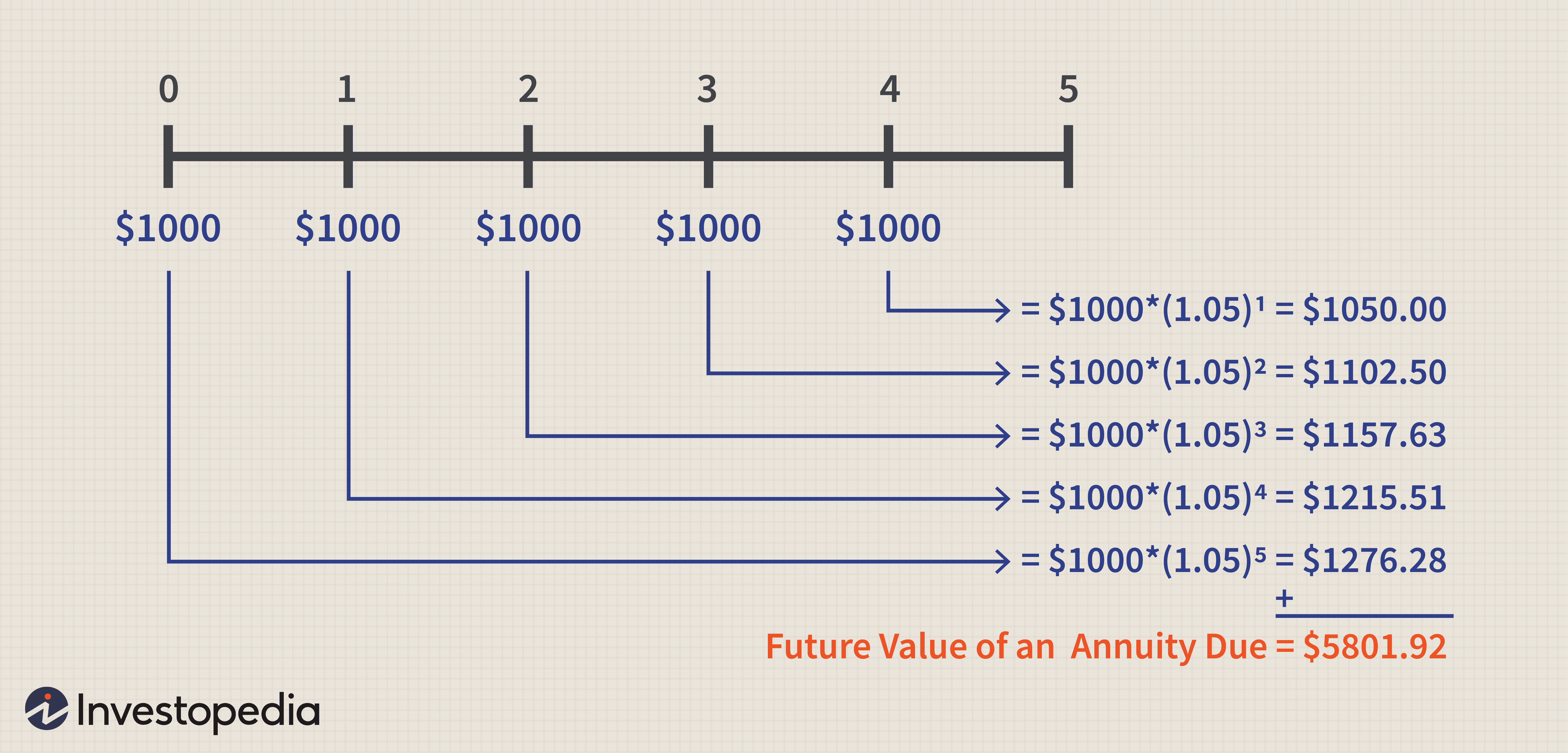
Компания будет получать поток из четырех денежных потоков, которые все являются единовременными выплатами. В некоторых ситуациях денежные потоки, возникающие в каждый период времени, составляют одинаковую сумму; другими словами. Денежные потоки равны в каждом периоде. Эти типы равномерных денежных потоков, происходящих через равные промежутки времени, например один раз в год. Известны как аннуитет. На следующем рисунке показан аннуитет. Состоящий из четырех выплат в размере 12 000 долларов США. Произведенных в конце каждого из четырех лет.

Характер денежных потоков—денежные потоки с одной суммой. Равномерные серии денежных потоков или неравномерные серии денежных потоков—по-разному влияют на формирование.
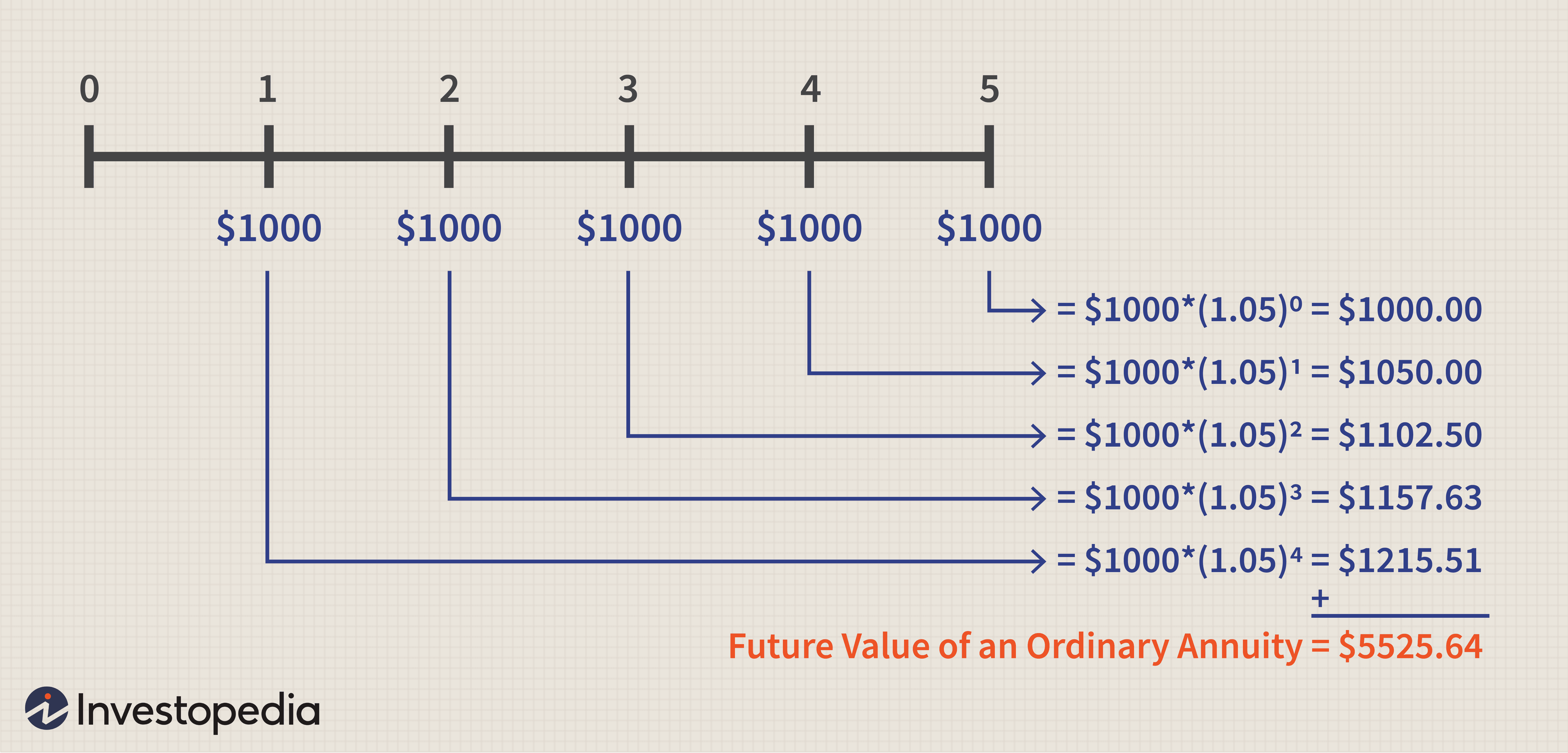
Компаундирование может применяться во многих типах финансовых операций. Таких как пополнение пенсионного счета или сберегательного счета колледжа. Предположим. Что физическое лицо вкладывает 10 000 долларов США в четырехлетний депозитный счет с сертификатом. Который выплачивает 10% процентов в конце каждого года (в данном случае 12/31). Любые проценты. Полученные в течение года. Будут удерживаться до конца четырехлетнего периода. А также будут начисляться 10% годовых.
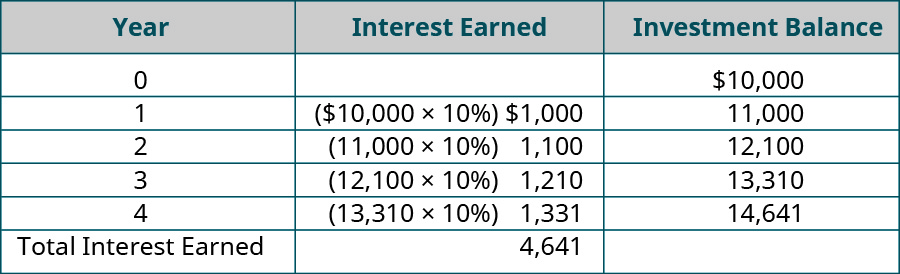
За счет эффекта сложения—начисления процентов на проценты—инвестор заработал 4641 доллар в процентах от четырехлетней инвестиции. Если бы инвестор снял заработанные проценты вместо того. Чтобы реинвестировать их на счет. Инвестор зарабатывал бы 1000 долларов в год в течение четырех лет или 4000 долларов процентов (10 000 × 10% = 1000 долларов в год × 4 года = 4000 долларов общих процентов). Комбинирование-это концепция. Которая используется для определения будущей стоимости (более подробные расчеты будущей стоимости будут рассмотрены далее в этом разделе). Но как насчет нынешней стоимости? Играет ли компаундирование роль в определении текущей стоимости? Термин, применяемый для определения приведенной стоимости. Называется дисконтированием.
Дисконтирование-это процедура. Используемая для расчета приведенной стоимости отдельного платежа или серии платежей. Которые будут получены в будущем. На основе предполагаемой процентной ставки или окупаемости инвестиций. Давайте рассмотрим простой пример. Чтобы объяснить концепцию дисконтирования.
Предположим. Что вы хотите накопить достаточно средств. Чтобы купить новый автомобиль. И что вам понадобится 5000 долларов через три года. Кроме того, предположим. Что ваши инвестированные средства будут зарабатывать 8% в год в течение трех лет. И вы реинвестируете любые проценты. Заработанные в течение трехлетнего периода. Если бы вы хотели снять достаточные средства со своего сберегательного счета для финансирования трехлетних инвестиций. Вам нужно было бы инвестировать 3969,16 долларов США сегодня и инвестировать их на счет. Зарабатывая 8% в течение трех лет. Через три года 3 969,16 доллара заработают 1 030,84 доллара и вырастут ровно до 5000 долларов, которые вам понадобятся. Это пример дисконтирования. Дисконтирование-это метод, с помощью которого мы берем будущую стоимость и определяем ее текущую или текущую стоимость. Понимание будущих приложений и расчетов стоимости поможет в понимании использования и расчетов текущей стоимости.
Есть преимущества в том. Чтобы инвестировать деньги сейчас в надежде на большую отдачу в будущем. Эти будущие доходы возможны благодаря процентным выплатам, полученным в качестве стимула для долгосрочного вложения денег. Знание того, какими будут эти будущие доходы, может помочь бизнесу решить. Оправдывают ли текущие инвестиции долгосрочный потенциал. Напомним, будущая стоимость (FV) определяется как стоимость инвестиции по истечении определенного периода времени. Будущая стоимость учитывает первоначальную инвестированную сумму. Период времени получения прибыли и процентную ставку по прибыли при расчете. Например, банк будет рассматривать будущую стоимость кредита на основе того. Соответствует ли долгосрочный клиент определенной процентной ставке при определении того. Следует ли одобрить кредит.
Чтобы определить будущую стоимость, банку понадобятся некоторые средства для определения будущей стоимости кредита. Банк может использовать формулы. Таблицы будущих значений. Финансовый калькулятор или приложение для работы с электронными таблицами. То же самое справедливо и для расчетов текущей стоимости. В связи с разнообразием калькуляторов и приложений для электронных таблиц мы представим определение как нынешних. Так и будущих значений с использованием таблиц. Сегодня на многих курсах колледжа эти таблицы используются в основном потому. Что они относительно просты для понимания при демонстрации материала. Для тех, кто предпочитает формулы. Различные формулы. Используемые для создания каждой таблицы. Печатаются в верхней части соответствующей таблицы. На многих занятиях по финансам вы узнаете. Как использовать формулы. Что касается использования финансового калькулятора. Хотя все они похожи. Руководство пользователя или быстрый поиск в Интернете предоставят конкретные указания для каждого финансового калькулятора. Что касается приложения для работы с электронными таблицами. Такого как Microsoft Excel. То существует несколько распространенных формул. Показанных на (рис.). Кроме того, В приложении C содержатся ссылки на видео и учебные пособия по использованию конкретных аспектов Excel. Таких как методы определения будущей и текущей стоимости.
| Формулы Excel | ||
|---|---|---|
| Компонент Значения Времени | Стенография формулы Excel | Подробная формула Excel |
| Приведенная Стоимость Единая Сумма | =PV | =PV(Ставка. Nта, FV) |
| Будущая Стоимость Одна Сумма | +FV | =FV(Ставка. Nта, PV) |
| Аннуитет по Текущей Стоимости | =PV | =PV(Тариф. Nта, FV, Тип) |
| Аннуитет Будущей Стоимости | =FV | =FV(Ставка. Nта, PV, Тип) |
| Чистая Приведенная Стоимость | =NPV | =NPV(ставка, CF2, CF3, CF4) + CF1 |
| Внутренняя норма прибыли | =IRR | =IRR(Инвестиции. CF1, CF2, CF3) |
| Ставка = годовая процентная ставка | ||
| N = количество периодов | ||
| Платеж = сумма годового платежа. Введенная в качестве отрицательного числа. Используйте 0 при расчете как текущей стоимости одной суммы. Так и будущей стоимости одной суммы | ||
| FV = будущая стоимость | ||
| PV = текущая или текущая стоимость | ||
| Тип = 0 для обычной ренты, 1 для причитающейся ренты | ||
| CF = денежный поток за период, таким образом, CF1 – период 1 денежного потока, CF2 – период 2 денежного потока и т.д. | ||
| Инвестирование = первоначальные инвестиции. Введенные в виде отрицательного числа | ||
Поскольку мы будем использовать таблицы в примерах в основной части главы, важно знать, что существует четыре возможных таблицы. Каждая из которых используется в определенных условиях ((рисунок).
| Таблица временной стоимости денег | |
|---|---|
| Ситуация | Заголовок таблицы |
| Будущая Стоимость – Единовременная Сумма | Будущая стоимость 1 доллар |
| Будущая стоимость – Аннуитет (равномерный поток платежей) | Будущая стоимость аннуитета |
| Приведенная Стоимость – Единовременная Сумма | Приведенная стоимость 1 долл. |
| Текущая стоимость – Аннуитет (равномерный поток платежей) | Текущая стоимость аннуитета |
В предыдущей ситуации банк использовал бы либо таблицу Будущей стоимости в 1 доллар США. Либо таблицу Будущей стоимости Обычной аннуитетной выплаты. Образцы которой приведены в Приложении B. Чтобы использовать правильную таблицу. Банку необходимо определить. Будет ли клиент возвращать их в конце срока кредита или периодически в течение всего срока кредита. Таблица Будущей стоимости в размере 1 доллара США используется. Если клиент вернет деньги в конце периода; если платежи будут производиться периодически в течение всего срока кредита. Они будут использовать Будущую стоимость таблицы аннуитета. Выбор правильной таблицы для использования имеет решающее значение для точного определения будущей стоимости. Применение в других деловых вопросах то же самое: бизнес должен также учитывать. Делают ли они инвестиции с погашением единовременной суммой или в структуре аннуитета. Прежде чем выбирать таблицу и производить расчет. В таблицах в столбцах показаны процентные ставки (i), а в строках-периоды (n). Столбцы процентных ставок представляют ожидаемую выплату процентной ставки по этим инвестициям. Процентные ставки могут основываться на опыте. Отраслевых стандартах. Ожиданиях федеральной налоговой политики и инвестициях в риски. Периоды представляют собой количество лет до получения платежа. Пересечение ожидаемых лет выплат и процентной ставки-это число. Называемое фактором будущей стоимости. Коэффициент будущей стоимости умножается на первоначальную инвестиционную стоимость для получения будущей стоимости ожидаемых денежных потоков (или инвестиционной прибыли).
Единовременный платеж-это приведенная стоимость инвестиций. Когда возврат произойдет в конце периода одним платежом. Для определения этого возврата используется таблица Будущего значения в размере 1 доллара.
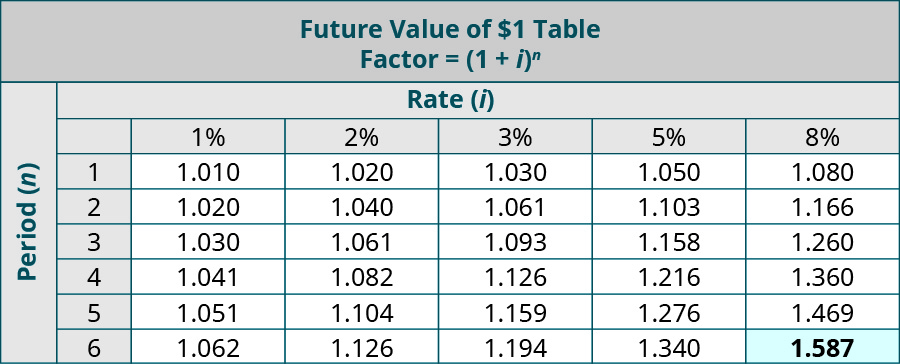
Например, вы откладываете деньги на отпуск. Который планируете провести через 6 лет. И хотите знать. Сколько принесут ваши первоначальные сбережения в будущем. Вы решаете разместить 4500 долларов США на инвестиционном счете сейчас, который приносит ожидаемую годовую прибыль в размере 8%. Взглянув на таблицу FV, n = 6 лет и i = 8%. Которые возвращают коэффициент будущей стоимости 1,587. Умножение этого коэффициента на первоначальную сумму инвестиций в размере 4500 долларов США дает 7141,50 доллара. Это означает. Что ваша первоначальная экономия в размере 4500 долларов составит примерно 7 141,50 доллара через 6 лет.
Обычный аннуитет-это такой. В котором платежи производятся в конце каждого периода равными частями. Будущая стоимость обычной ренты отражает стоимость текущих инвестиций в будущем. Если периодические платежи производились в течение всего срока действия серии.
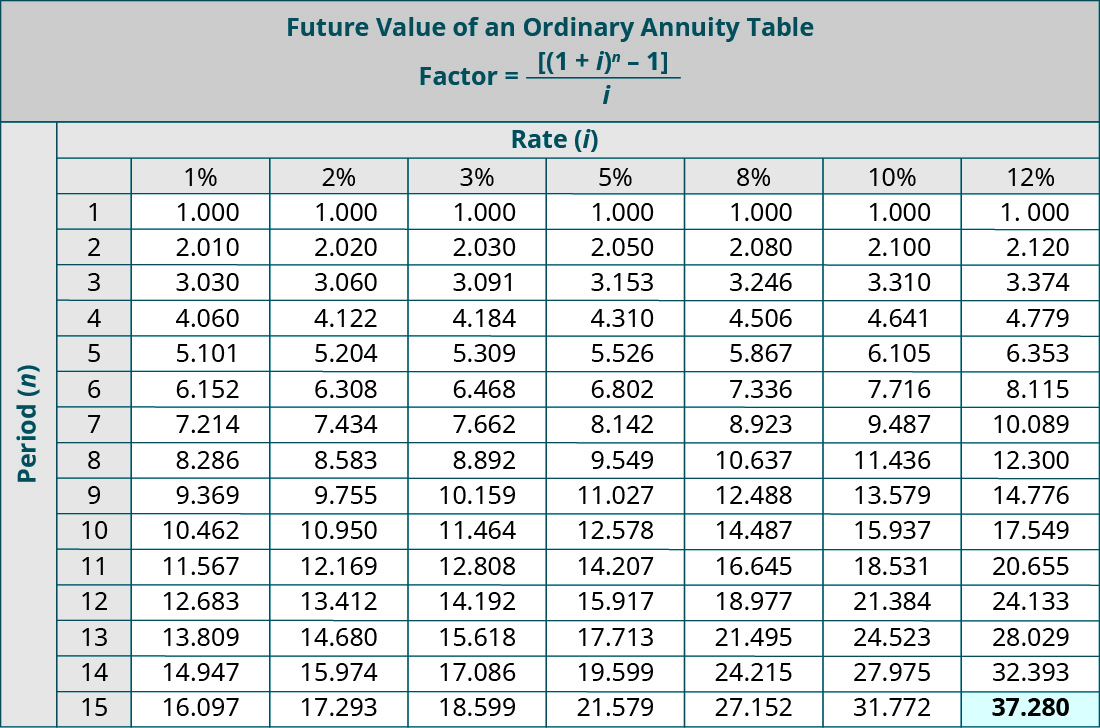
Например, вы откладываете деньги на пенсию и рассчитываете вносить 10 000 долларов в год в течение следующих 15 лет в пенсионный план 401(k). План предусматривает периодическую процентную доходность в размере 12%. Сколько будут стоить ваши инвестиции в будущем. Соответствующие этим критериям? В этом случае вы бы использовали Будущую стоимость Обычной таблицы аннуитетов. Соответствующий коэффициент. Где n = 15 и i = 12%. Равен 37.280. Умножение коэффициента на величину денежного потока дает будущую стоимость этих сбережений в рассрочку в размере (37,280 × 10 000 долларов США) 372 800 долларов США. Таким образом, вы можете ожидать, что ваши инвестиции составят 372 800 долларов США по истечении 15 лет, учитывая параметры.
Давайте теперь рассмотрим. Чем нынешняя стоимость отличается от будущей стоимости в использовании и вычислениях.
Определение Будущей Ценности
Определите будущую ценность для каждой из следующих ситуаций. При необходимости используйте таблицы будущих значений, приведенные в Приложении В, и округляйте ответы до ближайшего цента. Где это необходимо.
Solution
A. Use FV of $1 table. Future value factor where n = 7 and i = 5 is 1.407. 1.407 × 5,000 = $7,035. B. Use FV of an ordinary annuity table. Future value factor where n = 14 and i = 8 is 24.215. 24.215 × 11,500 = $278,472.50.
It is impossible to compare the value or potential purchasing power of the future dollar to today’s dollar; they exist in different times and have different values. Present value (PV) considers the future value of an investment expressed in today’s value. This allows a company to see if the investment’s initial cost is more or less than the future return. For example. A bank might consider the present value of giving a customer a loan before extending funds to ensure that the risk and the interest earned are worth the initial outlay of cash.
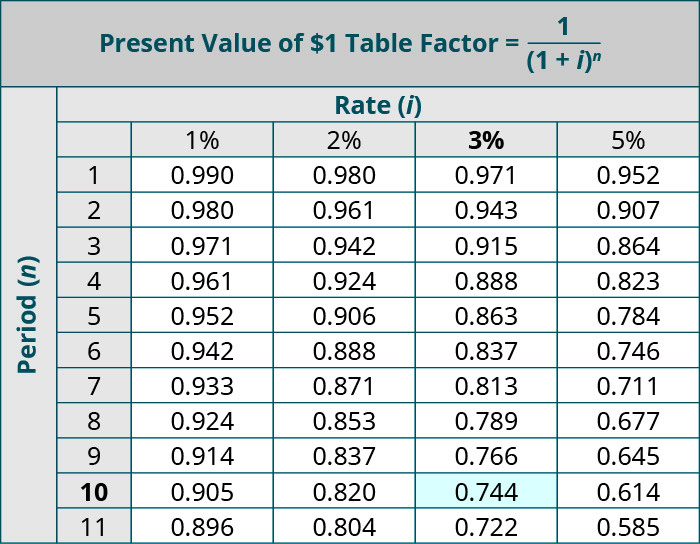
Similar to the Future Value tables, the columns show interest rates (i) and the rows show periods (n) in the Present Value tables. Periods represent how often interest is compounded (paid); that is, periods could represent days, weeks, months, quarters, years. Or any interest time period. For our examples and assessments. The period (n) will almost always be in years. The intersection of the expected payout years (n) and the interest rate (i) is a number called a present value factor. The present value factor is multiplied by the initial investment cost to produce the present value of the expected cash flows (or investment return).

The two tables provided in Appendix B for present value are the Present Value of $1 and the Present Value of an Ordinary Annuity. As with the future value tables, choosing the correct table to use is critical for accurate determination of the present value.
When referring to present value. The lump sum return occurs at the end of a period. A business must determine if this delayed repayment. With interest. Is worth the same as, more than. Or less than the initial investment cost. If the deferred payment is more than the initial investment. The company would consider an investment.
To calculate present value of a lump sum. We should use the Present Value of $1 table. For example. You are interested in saving money for college and want to calculate how much you would need put in the bank today to return a sum of $40,000 in 10 years. The bank returns an interest rate of 3% per year during these 10 years. Looking at the PV table, n = 10 years and i = 3% returns a present value factor of 0.744. Multiplying this factor by the return amount of $40,000 produces $29,760. This means you would need to put in the bank now approximately $29,760 to have $40,000 in 10 years.
As mentioned. To determine the present value or future value of cash flows. A financial calculator. A program such as Excel. Knowledge of the appropriate formulas. Or a set of tables must be used. Though we illustrate examples in the text using tables. We recognize the value of these other calculation instruments and have included chapter assessments that use multiple approaches to determining present and future value. Knowledge of different approaches to determining present and future value is useful as there are situations, such as having fractional interest rates, 8.45% for example. In which a financial calculator or a program such as Excel would be needed to accurately determine present or future value.
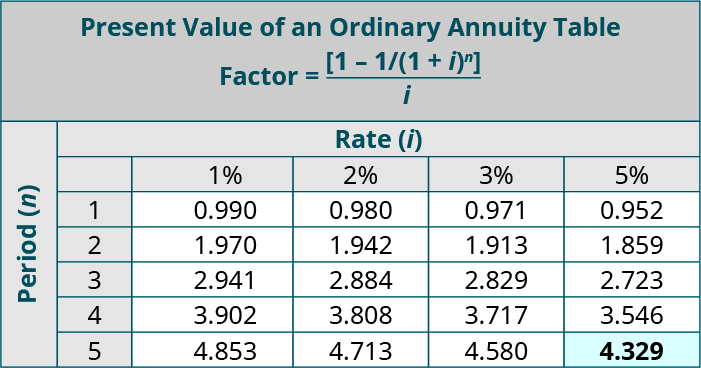
As discussed previously. Annuities are a series of equal payments made over time. And ordinary annuities pay the equal installment at the end of each payment period within the series. This can help a business understand how their periodic returns translate into today’s value.
For example. Assume that Sam needs to borrow money for college and anticipates that she will be able to repay the loan in $1,200 annual payments for each of 5 years. If the lender charges 5% per year for similar loans. How much cash would the bank be willing to lend Sam today? In this case. She would use the Present Value of an Ordinary Annuity table in Appendix B, where n = 5 and i = 5%. This yields a present value factor of 4.329. The current value of the cash flow each period is calculated as 4.329 × $1,200 = $5,194.80. Therefore, Sam could borrow $5,194.80 now given the repayment parameters.
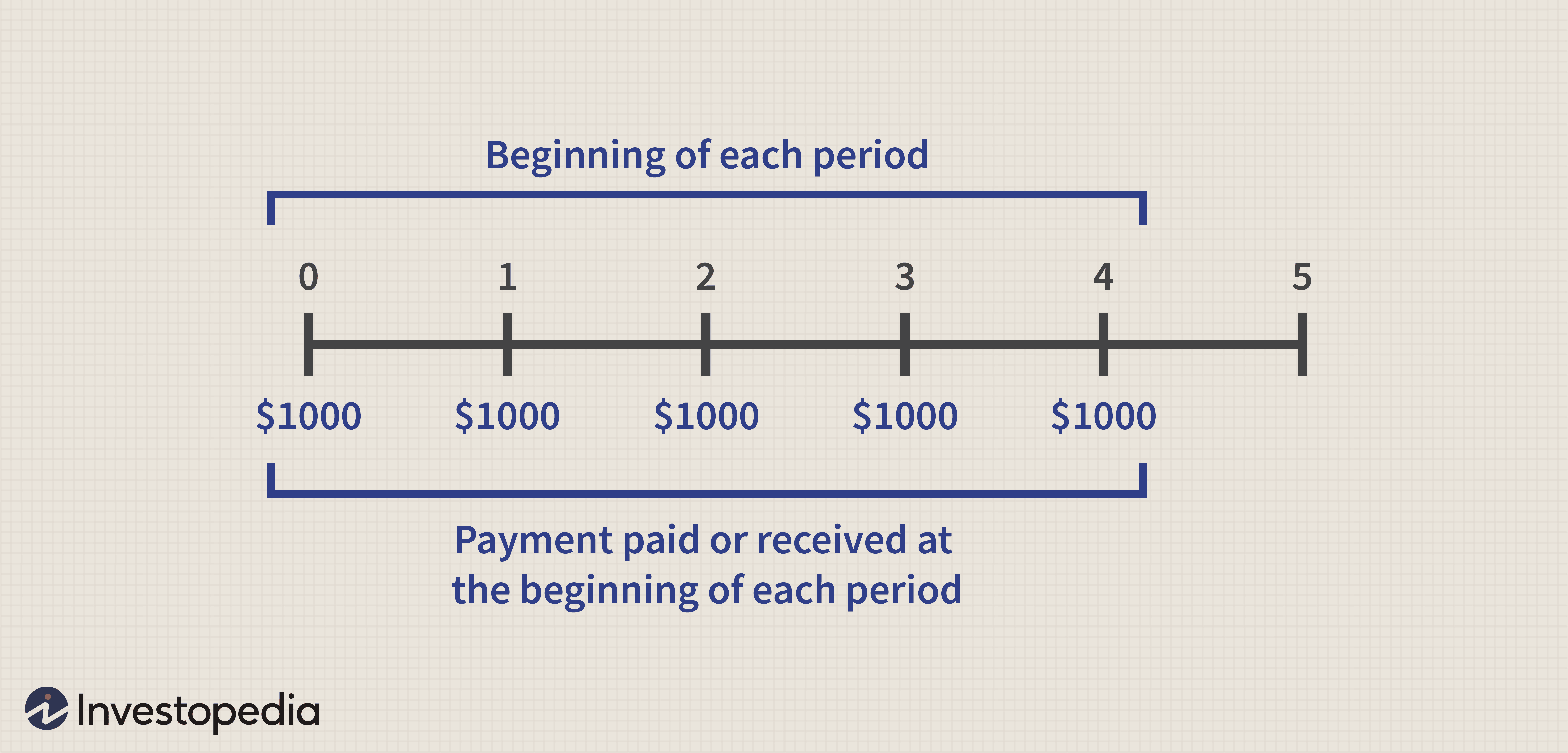
Our focus has been on examples of ordinary annuities (annuities due and other more complicated annuity examples are addressed in advanced accounting courses). With annuities due, the cash flow occurs at the start of the period. For example. If you wanted to deposit a lump sum of money into an account and make monthly rent payments starting today. The first payment would be made the same day that you made the deposit into the funding account. Because of this timing difference in the withdrawals from the annuity due. The process of calculating annuity due is somewhat different from the methods that you’ve covered for ordinary annuities.
Determining Present Value
Determine the present value for each of the following situations. Use the present value tables provided in Appendix B when needed. And round answers to the nearest cent where required.
Solution
a. Use PV of $1 table. Present value factor where n = 12 and i = 5 is 0.557. 0.557 × $100,000 = $55,700. b. Use PV of an ordinary annuity table. Present value factor where n = 8 and i = 3 is 7.020. 7.020 × $1,000 = $7,020.
For a lucky few. Winning the lottery can be a dream come true and the option to take a one-time payout or receive payments over several years does not seem to matter at the time. This lottery payout calculator shows how time value of money may affect your take-home winnings.