
Цели главы
Структура главы
Бюджетирование капитальных вложений по сравнению с текущими расходами
Классификация инвестиционных проектов
Экономическая оценка инвестиционных предложений
Чистая приведенная стоимость по сравнению с внутренней нормой прибыли
С учетом инфляции
Ключевые термины
Бюджетирование капитала имеет жизненно важное значение для принятия маркетинговых решений. Решения об инвестициях. Для принятия которых требуется время. Должны основываться на отдаче. Которую принесут эти инвестиции. Если проект не преследует исключительно социальные цели. Если инвестиции в долгосрочной перспективе убыточны. Неразумно инвестировать в него сейчас.

Часто было бы полезно знать. Какова текущая стоимость будущих инвестиций или сколько времени потребуется для их погашения (получения прибыли). Гораздо выгоднее было бы положить запланированные инвестиционные деньги в банк и получать проценты или инвестировать в альтернативный проект.
Типичные инвестиционные решения включают решение построить еще один зерновой элеватор. Хлопкоочистительный или холодильный склад или инвестировать в новое распределительное хранилище. На более низком уровне маркетологи, возможно. Пожелают оценить. Стоит ли больше тратить на рекламу или увеличить количество продавцов. Хотя трудно измерить соотношение продаж к рекламе.
Эта глава предназначена для того. Чтобы обеспечить:
· Понимание важности составления бюджета капитальных вложений в принятии маркетинговых решений
· Объяснение различных типов инвестиционных проектов
· Введение в экономическую оценку инвестиционных предложений
· Важность концепции и расчета чистой приведенной стоимости и внутренней нормы прибыли при принятии решений
· Преимущества и недостатки метода окупаемости как метода первоначального отбора двух или более конкурирующих проектов.
Бюджетирование капитала, безусловно. Является жизненно важной деятельностью в бизнесе. Огромные суммы денег могут быть легко потрачены впустую. Если инвестиции окажутся неправильными или неэкономичными. Предмет исследования трудно понять в силу природы охватываемой темы. А также из-за математического содержания. Тем не менее. Он стремится опираться на концепцию будущей стоимости денег. Которые могут быть потрачены сейчас. Для этого он изучает методы чистой приведенной стоимости. Внутренней нормы прибыли и аннуитетов. Сроки поступления денежных средств важны при принятии новых инвестиционных решений. Поэтому в этой главе рассматривается концепция

Одной из проблем. Которая беспокоит развивающиеся страны. Являются Глава заканчивается показом того. Как маркетологи могут принять это во внимание.
Проект капитальных вложений можно отличить от текущих расходов по двум признакам:
а) такие проекты являются относительно крупными
б) между инвестиционными затратами и получением выгод проходит значительный промежуток времени (более одного года)..
В результате большинство средних и крупных организаций разработали специальные процедуры и методы для принятия этих решений.

Системный подход к составлению бюджета капитальных вложений подразумевает:
а) формулирование долгосрочных целей
б) творческий поиск и выявление новых инвестиционных возможностей
в) классификация проектов и признание экономически и/или статистически зависимых предложений
d) оценка и прогнозирование текущих и будущих денежных потоков
e) надлежащая административная структура. Способная передавать необходимую информацию на уровень принятия решений
f) контроль за расходами и тщательный мониторинг важнейших аспектов выполнения проекта
g) требуется набор правил принятия решений. Которые могут отличать приемлемые альтернативы от неприемлемых.
Последний пункт (g) имеет решающее значение. И это тема последующих разделов главы.
а) По размеру проекта
Небольшие проекты могут быть одобрены руководителями департаментов. Более тщательный анализ и одобрение Совета директоров необходимы для крупных проектов, скажем. На полмиллиона долларов или более.
б) По видам льгот для фирмы
· увеличение денежного потока
· снижение риска
· косвенная выгода (душевые для работников и т. Д.).
в) По степени зависимости
· взаимоисключающие проекты (может выполнять проект A или B, но не оба)
· дополнительные проекты: принятие проекта А увеличивает денежный поток проекта В.
· замещающие проекты: принятие проекта А уменьшает денежный поток проекта В.
г) По степени статистической зависимости
· Положительная зависимость
· Отрицательная зависимость
· Статистическая независимость.
д) По видам денежных потоков
· Обычный денежный поток: только одно изменение в знаке денежного потока
например. – / + + + + или + / – – – – и т. Д
· Нетрадиционные денежные потоки: более одного изменения в знаке движения денежных средств,
например, + / – / + + + или -/+/-/++++, и т.д.
Анализ предусматривает правило принятия решений для:
I) принятие или
II) отклонениеинвестиционные проекты
Временная ценность денег
Напомним. Что взаимодействие кредиторов с заемщиками устанавливает равновесную процентную ставку. Заимствование имеет смысл только в том случае. Если доходность по кредиту превышает стоимость заемных средств. Кредитование имеет смысл только в том случае. Если доходность по крайней мере равна доходности. Которую можно получить от альтернативных возможностей в том же классе рисков.
Процентная ставка. Полученная кредитором. Складывается из:
i) Временная ценность денег: получение денег предпочтительнее раньше, чем позже.
Деньги можно использовать. Чтобы заработать больше денег. Чем раньше будут получены деньги. Тем больше потенциал для увеличения богатства. Таким образом. Чтобы отказаться от использования денег. Вы должны получить некоторую компенсацию.
ii) Риск невозврата суммы основного капитала. Эта неопределенность требует премии в качестве хеджирования риска. Следовательно. Доходность должна быть соизмерима с принимаемым риском.
iii) Инфляция: со временем деньги могут потерять свою покупательную способность. Кредитору должна быть выплачена компенсация за снижение расходной/покупательной способности денег.
Если кредитор не получит компенсации. Ему/ей будет хуже. Когда кредит будет погашен. Чем в момент предоставления денег.
а) Будущие ценности/сложные проценты
Будущая стоимость (FV) – это стоимость в долларах в какой-то момент в будущем одной или нескольких инвестиций.
FV состоит из:
i) первоначальная сумма вложенных денег и
ii) доход в виде процентов.
Общая формула для вычисления будущей стоимости выглядит следующим образом:
nFV = Vo (l + r)n
где
V o-начальная инвестированная сумма
r-процентная ставка
n-количество периодов. За которые инвестиции должны получать проценты.
Таким образом. Мы можем вычислить будущую стоимость того. Что V o будет накапливаться в течение n лет. Когда она будет ежегодно увеличиваться с той же скоростью r. Используя приведенную выше формулу.
Теперь попробуйте выполнить упражнение 6.1.
Упражнение 6.1 Будущие ценности/сложные проценты
i) Какова будущая стоимость 10 долларов. Инвестированных под 10% в конце 1 года?
ii) Какова будущая стоимость 10 долларов. Инвестированных под 10% в конце 5 лет?
Мы можем получить приведенную стоимость (PV). Используя формулу:
nFV = Vo(I + r)n
Обозначая V o через PV, мы получаем:
FVn = PV (I + r)n
разделив обе стороны формулы на (I + r)n, мы получим:

Обоснование формулы:
Как вы увидите из следующего упражнения. Учитывая альтернативу заработка 10% на своих деньгах. Физическое лицо (или фирма) никогда не должно предлагать (инвестировать) более 10,00 долларов. Чтобы получить 11,00 долларов с уверенностью в конце года.
Теперь попробуйте выполнить упражнение 6.2
Упражнение 6.2 Приведенная стоимость
i) Какова текущая стоимость в размере 11,00 долл. США на конец одного года?
ii) Каков PV в размере 16,10 доллара США по истечении 5 лет?
б) Чистая приведенная стоимость (NPV)
Метод NPV используется для оценки желательности инвестиций или проектов.
где:
C t = чистое поступление денежных средств в конце года t
I o = первоначальные инвестиционные затраты
r = ставка дисконтирования/требуемая минимальная норма прибыли на инвестиции
n = продолжительность проекта/инвестиций в годах.
Коэффициент дисконтирования r может быть рассчитан с использованием:
Примеры:
N. B. На этом этапе преподаватель должен представить таблицы чистой приведенной стоимости из любого признанного опубликованного источника. Сделай это сейчас.
Правило принятия решений:
Если NPV положительный (+): примите проект
Если NPV отрицательный(-): отклонить проект
Теперь попробуйте выполнить упражнение 6.3.
Упражнение 6.3 Чистая приведенная стоимость
Фирма намерена инвестировать 1000 долларов США в проект, который принес чистые поступления в размере 800, 900 и 600 долларов США в первый. Второй и третий годы соответственно. Должна ли фирма продолжать реализацию проекта?
Сначала попробуйте выполнить расчет без ссылки на таблицы чистой приведенной стоимости.
в) Аннуитеты
N. B. Познакомьте студентов с таблицами аннуитетов из любого признанного опубликованного источника.
Набор денежных потоков. Которые равны в каждом периоде. Называется аннуитетом.
Пример:
|
Год |
Денежный поток ($) |
|
0 |
-800 |
|
1 |
400 |
|
2 |
400 |
|
3 |
400 |
PV = $400(0.9091) + $400(0.8264) + $400(0.7513)
= $363.64 + $330.56 + $300.52
= $994.72
NPV = $994,72 – $800,00
= $194.72
Альтернативно,
PV аннуитета = 400 долларов США (PVFAt.i) (3,0,10)
= $400 (0.9091 + 0.8264 + 0.7513)
= 400 долларов х 2,4868
= $994.72
NPV = $994,72 – $800,00
= $194.72
d) Вечность
Бессрочный срок-это аннуитет с бесконечной жизнью. Это равная сумма денег. Которая должна быть выплачена в каждый период навсегда.
где:
C – сумма, подлежащая получению за период
r – ставка дисконтирования или процентная ставка
Пример:
Вам обещают бессрочный доход в размере 700 долларов в год по ставке 15% годовых. Какую цену (PV) вы должны быть готовы заплатить за этот доход?
= $4,666.67
Вечность с ростом:
Предположим. Что годовой доход в размере 700 долларов. Полученный в последний раз. Как ожидается. Будет расти со скоростью 5% в год (в совокупности) навсегда. Во сколько обойдется этот доход. Если дисконтировать его на 15%?
Решение:
Вычтите темп роста из ставки дисконтирования и рассматривайте денежный поток первого периода как бессрочный.
= $735/0.10
= $7,350
e) Внутренняя норма прибыли (IRR)
Обратитесь к таблицам студентов в любом признанном опубликованном источнике.
· IRR-это ставка дисконтирования. При которой NPV для проекта равен нулю. Эта ставка означает. Что приведенная стоимость притока денежных средств по проекту будет равна приведенной стоимости его оттока.
· IRR-это безубыточная ставка дисконтирования.
· IRR определяется методом проб и ошибок.
где r = IRR
IRR аннуитета:
где:
Q (n,r) – коэффициент дисконтирования
o I – это первоначальные затраты
C-это единый годовой чек (C 1 = C 2 =…. = C n).
Пример:
Каков IRR равного годового дохода в размере 20 долларов США в год. Который начисляется в течение 7 лет и стоит 120 долларов?
= 6
Из таблиц = 4%
Экономическое обоснование IRR:
Если IRR превышает стоимость капитала. Проект стоит того. Т. е. его выгодно осуществлять. Теперь попробуйте выполнить упражнение 6.4
Упражнение 6.4 Внутренняя норма прибыли
Найдите рентабельность этого проекта для фирмы с 20% – ной стоимостью капитала:
|
ГОД |
ДЕНЕЖНЫЙ ПОТОК |
|
$ |
|
|
0 |
-10,000 |
|
1 |
8,000 |
|
2 |
6,000 |
а) Попробуйте 20%
б) Попробуйте 27%
в) Попробуйте 29%
Независимые и зависимые проекты
Методы NPV и IRR тесно связаны. Потому что:
i) оба являются скорректированными по времени показателями прибыльности, и
ii) их математические формулы почти идентичны.
Итак, какой метод приводит к оптимальному решению: IRR или NPV?
a) NPV против IRR: Независимые проекты
Независимый проект: Выбор одного проекта не исключает выбора другого.
При обычных денежных потоках (-|+|+) не возникает конфликта в принятии решений; в этом случае как NPV. Так и IRR приводят к одинаковым решениям о принятии/отклонении.
Рисунок 6.1 NPV против IRR Независимые проекты

Если денежные потоки дисконтированы по k 11: принять проект.
Если денежные потоки дисконтированы по k 2, NPV отрицательный, а IRR
Математическое доказательство: для того. Чтобы проект был приемлемым. NPV должен быть положительным, т. е.
Аналогично для того же проекта. Чтобы быть приемлемым:

где R-IRR.
Поскольку числители C t идентичны и положительны в обоих случаях:
·
· Если NPV = 0, то R = k: компания равнодушна к такому проекту;
· Следовательно. IRR и NPV в данном случае приводят к одному и тому же решению.
b) NPV против IRR: Зависимые проекты
NPV сталкивается с IRR там. Где существуют взаимоисключающие проекты.
Пример:
Компания Доступна следующая информация:
|
Первоначальные Инвестиционные Затраты |
Чистый приток на конец года |
|
|
Проект А |
-9,500 |
11,500 |
|
Проект В |
-15,000 |
18,000 |
Предположим. Что k = 10%. Какой проект должен осуществить Агротекс?
= $954.55
= $1,363.64
Оба проекта рассчитаны на один год:
IRRA:
11 500 долларов = 9 500 долларов (1 +R A)
= 1.21-1
следовательно, IRR A = 21%
IRRB:
$18 000 = $15 000(1 + R B)
= 1.2-1
следовательно, IRR B = 20%
Решение:
Предполагая. Что k = 10%. Оба проекта приемлемы. Потому что:
NPV A и NPV B являются положительными
IRR AB
Какой проект является
Если мы используем метод NPV:
NPV BA (954,55 доллара США): Агротекс должен выбрать проект B.
Если мы используем метод IRR:
IRR AB (20%): Агротекс должен выбрать проект A. См. рисунок 6.2.
Рисунок 6.2 NPV против IRR: Зависимые проекты

До ставки дисконтирования k o: проект B превосходит проект A. Поэтому проект B предпочтительнее проекта A.
За пределами точки к о: проект А превосходит проект В. Поэтому проект А предпочтительнее проекта В
Эти два метода не оценивают проекты одинаково.
Различия в масштабах инвестиций
NPV и IRR могут привести к противоречивым решениям в тех случаях. Когда проекты отличаются масштабом инвестиций. Пример:
|
Годы |
0 |
1 |
2 |
3 |
|
Проект А |
-2,500 |
1,500 |
1,500 |
1,500 |
|
Проект В |
-14,000 |
7,000 |
7,000 |
7,000 |
Предположим. Что k= 10%.
NPV = 1500 долларов США x PVFA под 10% в течение 3 лет
= 1500 долларов США x 2.487
= $3,730.50 – $2,500.00
= $1,230.50.B NPV == $7,000 x PVFA под 10% в течение 3 лет
= $7,000 x 2.487
= $17,409 – $14,000
= $3,409.00.IRRA =
= 1.67.
Следовательно, IRR A = 36% (из таблиц)
IRRB=
= 2.0
Следовательно, IRR B = 21%
Решение:
Противоречащие, как:
· NPV предпочитает B A
· IRR предпочитает A B
|
NPV |
IRR |
|
|
Проект А |
$ 3,730.50 |
36% |
|
Проект В |
$17,400.00 |
21% |
См. рис. 6.3.
Рисунок 6.3 Масштабы инвестиций

Чтобы показать, почему:
i) NPV предпочитает B. Более крупный проект. Для ставки дисконтирования ниже 20%
ii) NPV превосходит IRR
а) Используйте подход с добавочным денежным потоком. Подход
б) Выбор проекта В равнозначен выбору гипотетического проекта
|
0 |
1 |
2 |
3 |
|
|
Проект В |
– 14,000 |
7,000 |
7,000 |
7,000 |
|
Проект А |
– 2,500 |
1,500 |
1,500 |
1,500 |
|
– 11,500 |
5,500 |
5,500 |
5,500 |
IRR
= 2.09
= 20%
c) Выбор B эквивалентен: A + (B – A) = B
d) Выбор более крупного проекта B означает выбор меньшего проекта A плюс дополнительные расходы в размере 11 500 долларов США. Из которых 5500 долларов США будут реализовываться каждый год в течение следующих 3 лет.
e) IRR для дополнительного денежного потока составляет 20%.
f) Учитывая k в размере 10%. Это выгодная возможность. Поэтому ее необходимо принять.
g) Но, если бы k было больше. Чем IRR (20%) при увеличении CF. Тогда отклоните проект.
h) В точке пересечения,
NPV A = NPV B или NPV A – NPV B = 0, т. е. безразлично к проектам A и B.
i) Если k = 20% (IRR от
· Это оправдывает использование критерия NPV.
Преимущество NPV:
· Это гарантирует. Что фирма достигнет оптимального масштаба инвестиций.
Недостаток IRR:
· It expresses the return in a percentage form rather than in terms of absolute dollar returns. E.g. the IRR will prefer 500% of $1 to 20% return on $100. However, most companies set their goals in absolute terms and not in % terms. E.g. target sales figure of $2.5 million.
The timing of the cash flow
The IRR may give conflicting decisions where the timing of cash flows varies between the 2 projects.
Note that initial outlay Io is the same.
|
0 |
1 |
2 |
|
|
Project A |
– 100 |
20 |
125.00 |
|
Project B |
– 100 |
100 |
31.25 |
|
“A minus B” |
0 |
– 80 |
88.15 |
Assume k = 10%
|
NPV |
IRR |
|
|
Project A |
17.3 |
20.0% |
|
Project B |
16.7 |
25.0% |
|
“A minus B” |
0.6 |
10.9% |
IRR prefers B to A even though both projects have identical initial outlays. So, the decision is to accept A. That is B + (A – B) = A. See figure 6.4.
Figure 6.4 Timing of the cash flow

The horizon problem
NPV and IRR rankings are contradictory. Project A earns $120 at the end of the first year while project B earns $174 at the end of the fourth year.
|
0 |
1 |
2 |
3 |
4 |
|
|
Project A |
-100 |
120 |
– |
– |
– |
|
Project B |
-100 |
– |
– |
– |
174 |
Assume k = 10%
|
NPV |
IRR |
|
|
Project A |
9 |
20% |
|
Project B |
19 |
15% |
Decision:
NPV prefers B to A
IRR prefers A to B.
The profitability index – PI
This is a variant of the NPV method.
Decision rule:
PI > 1; accept the project
PIIf NPV = 0, we have:
NPV = PV – Io = 0
PV = IoDividing both sides by Io we get:
PI of 1.2 means that the project’s profitability is 20%. Example:
PV of CF
Io
PI
Project A
100
50
2.0
Project B
1,500
1,000
1.5
Decision:
Choose option B because it maximises the firm’s profitability by $1,500.
Disadvantage of PI:
Like IRR it is a percentage and therefore ignores the scale of investment.
The payback period (PP)
The CIMA defines payback as ‘the time it takes the cash inflows from a capital investment project to equal the cash outflows. Usually expressed in years’. When deciding between two or more competing projects. The usual decision is to accept the one with the shortest payback.
Payback is often used as a “first screening method”. By this, we mean that when a capital investment project is being considered. The first question to ask is: ‘How long will it take to pay back its cost?’ The company might have a target payback. And so it would reject a capital project unless its payback period were less than a certain number of years.
Example 1:
Years
0
1
2
3
4
5
Project A
1,000,000
250,000
250,000
250,000
250,000
250,000
For a project with equal annual receipts:
= 4 years
Example 2:
Years
0
1
2
3
4
Project B
– 10,000
5,000
2,500
4,000
1,000
Payback period lies between year 2 and year 3. Sum of money recovered by the end of the second year
= $7,500, i.e. ($5,000 + $2,500)
Sum of money to be recovered by end of 3rd year
= $10,000 – $7,500
= $2,500
= 2.625 years
Disadvantages of the payback method:
· It ignores the timing of cash flows within the payback period. The cash flows after the end of payback period and therefore the total project return.
· It ignores the time value of money. This means that it does not take into account the fact that $1 today is worth more than $1 in one year’s time. An investor who has $1 today can either consume it immediately or alternatively can invest it at the prevailing interest rate, say 30%. To get a return of $1.30 in a year’s time.
· It is unable to distinguish between projects with the same payback period.
· It may lead to excessive investment in short-term projects.
Advantages of the payback method:
· Payback can be important: long payback means capital tied up and high investment risk. The method also has the advantage that it involves a quick. Simple calculation and an easily understood concept.
The accounting rate of return – (ARR)
The ARR method (also called the return on capital employed (ROCE) or the return on investment (ROI) method) of appraising a capital project is to estimate the accounting rate of return that the project should yield. If it exceeds a target rate of return. The project will be undertaken.
Note that net annual profit excludes depreciation.
Example:
A project has an initial outlay of $1 million and generates net receipts of $250,000 for 10 years.
Assuming straight-line depreciation of $100,000 per year:
= 15%
= 30%
Disadvantages:
· It does not take account of the timing of the profits from an investment.
· It implicitly assumes stable cash receipts over time.
· It is based on accounting profits and not cash flows. Accounting profits are subject to a number of different accounting treatments.
· It is a relative measure rather than an absolute measure and hence takes no account of the size of the investment.
· It takes no account of the length of the project.
· it ignores the time value of money.
The payback and ARR methods in practice
Despite the limitations of the payback method. It is the method most widely used in practice. There are a number of reasons for this:
· It is a particularly useful approach for ranking projects where a firm faces liquidity constraints and requires fast repayment of investments.
· It is appropriate in situations where risky investments are made in uncertain markets that are subject to fast design and product changes or where future cash flows are particularly difficult to predict.
· The method is often used in conjunction with NPV or IRR method and acts as a first screening device to identify projects which are worthy of further investigation.
· it is easily understood by all levels of management.
· It provides an important summary method: how quickly will the initial investment be recouped?
Now attempt exercise 6.5.
Exercise 6.5 Payback and ARR
Delta Corporation is considering two capital expenditure proposals. Both proposals are for similar products and both are expected to operate for four years. Only one proposal can be accepted.
The following information is available:
Profit/(loss)
Proposal A
Proposal B
$
$
Initial investment
46,000
46,000
Year 1
6,500
4,500
Year 2
3,500
2,500
Year 3
13,500
4,500
Year 4
Loss 1,500
Profit 14,500
Estimated scrap value at the end of Year 4
4,000
4,000
Depreciation is charged on the straight line basis. Problem:
a) Calculate the following for both proposals:
i) the payback period to one decimal place
ii) the average rate of return on initial investment. To one decimal place.So far, the effect of inflation has not been considered on the appraisal of capital investment proposals. Inflation is particularly important in developing countries as the rate of inflation tends to be rather high. As inflation rate increases. So will the minimum return required by an investor. For example. One might be happy with a return of 10% with zero inflation. But if inflation was 20%. One would expect a much greater return.
Example:
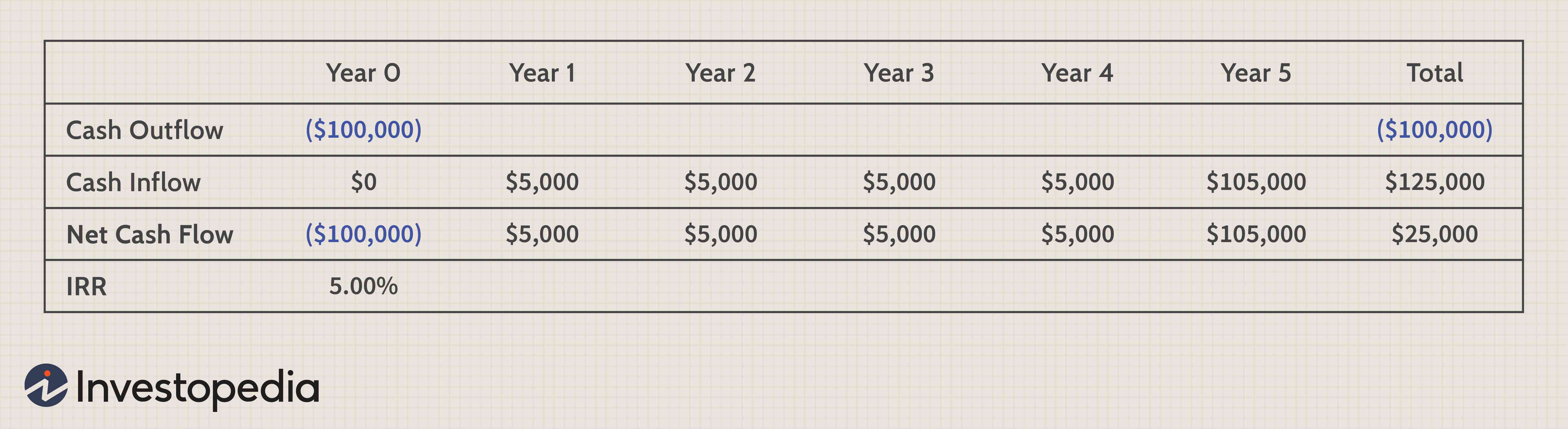
Keymer Farm is considering investing in a project with the following cash flows:
TIME
ACTUAL CASH FLOWS
Z$
0
(100,000)
1
90,000
2
80,000
3
70,000
Keymer Farm requires a minimum return of 40% under the present conditions. Inflation is currently running at 30% a year. And this is expected to continue indefinitely. Should Keymer Farm go ahead with the project?
Let us take a look at Keymer Farm’s required rate of return. If it invested $10,000 for one year on 1 January. Then on 31 December it would require a minimum return of $4,000. With the initial investment of $10,000, the total value of the investment by 31 December must increase to $14,000. During the year. The purchasing value of the dollar would fall due to inflation. We can restate the amount received on 31 December in terms of the purchasing power of the dollar at 1 January as follows:
Amount received on 31 December in terms of the value of the dollar at 1 January:
= $10,769
In terms of the value of the dollar at 1 January. Keymer Farm would make a profit of $769 which represents a rate of return of 7.69% in “today’s money” terms. This is known as the real rate of return. The required rate of 40% is a money rate of return (sometimes known as a nominal rate of return). The money rate measures the return in terms of the dollar. Which is falling in value. The real rate measures the return in constant price level terms.
The two rates of return and the inflation rate are linked by the equation:
(1 + money rate) = (1 + real rate) x (1 + inflation rate)
where all the rates are expressed as proportions.
In the example,
(1 + 0.40) = (1 + 0.0769) x (1 + 0.3)
= 1.40
So, which rate is used in discounting? As a rule of thumb:
a) If the cash flows are expressed in terms of actual dollars that will be received or paid in the future. The money rate for discounting should be used.
b) If the cash flows are expressed in terms of the value of the dollar at time 0 (i.e. in constant price level terms). The real rate of discounting should be used.
In Keymer Farm’s case. The cash flows are expressed in terms of the actual dollars that will be received or paid at the relevant dates. Therefore, we should discount them using the money rate of return.
TIME
CASH FLOW
DISCOUNT FACTOR
PV
$
40%
$
0
(150,000)
1.000
(100,000)
1
90,000
0.714
64,260
2
80,000
0.510
40,800
3
70,000
0.364
25,480
30,540
The project has a positive net present value of $30,540, so Keymer Farm should go ahead with the project.
The future cash flows can be re-expressed in terms of the value of the dollar at time 0 as follows. Given inflation at 30% a year:
TIME
ACTUAL CASH FLOW
CASH FLOW AT TIME 0 PRICE LEVEL
$
$
0
(100,000)
(100,000)
1
90,000
69,231
2
80,000
47,337
3
70,000
31,862
The cash flows expressed in terms of the value of the dollar at time 0 can now be discounted using the real value of 7.69%.
TIME
CASH FLOW
DISCOUNT FACTOR
PV
$
7.69%
$
0
(100,000)
1.000
(100,000)
1
69,231
64,246
2
47,337
40,804
3
31,862
25,490
30,540
The NPV is the same as before.
Expectations of inflation and the effects of inflation
When a manager evaluates a project. Or when a shareholder evaluates his/her investments. He/she can only guess what the rate of inflation will be. These guesses will probably be wrong. At least to some extent. As it is extremely difficult to forecast the rate of inflation accurately. The only way in which uncertainty about inflation can be allowed for in project evaluation is by risk and uncertainty analysis.
Inflation may be general, that is. Affecting prices of all kinds, or specific to particular prices. Generalised inflation has the following effects:
a) Inflation will mean higher costs and higher selling prices. It is difficult to predict the effect of higher selling prices on demand. A company that raises its prices by 30%. Because the general rate of inflation is 30%. Might suffer a serious fall in demand.
b) Inflation. As it affects financing needs. Is also going to affect gearing. And so the cost of capital.
c) Since fixed assets and stocks will increase in money value. The same quantities of assets must be financed by increasing amounts of capital. If the future rate of inflation can be predicted with some degree of accuracy. Management can work out how much extra finance the company will need and take steps to obtain it. E.g. by increasing retention of earnings. Or borrowing.
However, if the future rate of inflation cannot be predicted with a certain amount of accuracy. Then management should estimate what it will be and make plans to obtain the extra finance accordingly. Provisions should also be made to have access to ‘contingency funds’ should the rate of inflation exceed expectations. E.g. a higher bank overdraft facility might be arranged should the need arise.
Many different proposals have been made for accounting for inflation. Two systems known as “Current purchasing power” (CPP) and “Current cost accounting” (CCA) have been suggested.
CPP is a system of accounting which makes adjustments to income and capital values to allow for the general rate of price inflation.
CCA is a system which takes account of specific price inflation (i.e. changes in the prices of specific assets or groups of assets). But not of general price inflation. It involves adjusting accounts to reflect the current values of assets owned and used.
At present, there is very little measure of agreement as to the best approach to the problem of ‘accounting for inflation’. Both these approaches are still being debated by the accountancy bodies.
Now attempt exercise 6.6.
Exercise 6.6 Inflation
TA Holdings is considering whether to invest in a new product with a product life of four years. The cost of the fixed asset investment would be $3,000,000 in total. With $1,500,000 payable at once and the rest after one year. A further investment of $600,000 in working capital would be required.
The management of TA Holdings expect all their investments to justify themselves financially within four years. After which the fixed asset is expected to be sold for $600,000.
The new venture will incur fixed costs of $1,040,000 in the first year. Including depreciation of $400,000. These costs. Excluding depreciation. Are expected to rise by 10% each year because of inflation. The unit selling price and unit variable cost are $24 and $12 respectively in the first year and expected yearly increases because of inflation are 8% and 14% respectively. Annual sales are estimated to be 175,000 units.
TA Holdings money cost of capital is 28%.
Is the product worth investing in?
Accounting rate of return
Annuities
Capital budgeting
Cash flow
Classification of investment projects
Compound interest
Current cost accounting (CCA)
Current purchasing power (CPP)
Dependent projects
Independent projects
Inflation
Interest rate
Internal rate of return
Investment decision
Net present value
Payback period
Perpetuity
Present value
Rates of return
The time value of money